Sistemas y lenguajes de programación

Tipos de sistemas y lenguajes de programación

- Sistema binario (0,1) > uso de 1 y 0 en combinación
para expresar números y operaciones

-Sistema decimal (0,9) > el sistema común

-Sistema octal (0,7) > uso del 0 al 7 para expresar números
y operaciones, con el 7 como el numero mayor posible cuando se habla de unidad.

-Sistema hexadecimal (0,F) uso del 0 a la F con 9 como el
número mayor posible cuando se habla de unidad y F como letra mayor a la cual
le sigue el 10.

Operaciones con los sistemas:

La suma en los sistemas se realiza de forma común, usando
los límites establecidos por cada sistema. Luego de pasar el límite en la
unidad del número se pasa a la menor combinación de números siguientes posibles.

Ejemplos:

En el sistema binario:

1+1=10; 1+1+1=11; 1+1+1+1=100

En el sistema decimal:

9+3=12; 9+20=29; 6+5=11

En el sistema octal:

7+1=10; 7+3=12;
7+5=14

En el sistema hexadecimal:

9+1=A; F+3=12; F+10=19

La resta se realiza de la forma inversa en la mayoría de

los sistemas, exceptuando el binario. Donde se realiza una tabla para la resta:

Donde (p) significa préstamo, al igual que en las restas
simples con los números de un sistema decimal.

Ejemplos:

10001-01010=00111; 11011001-10101011=00101110

Teorema fundamental de la numeración

Se utiliza para convertir los números de los sistemas
octales y hexadecimales a números en sistema decimal. Se da por:

…X3B^3+X2B^2+X1B^1+X0B^0+X-1B^-1+X-2B^-2+X-3B^-3…

Por ejemplo: 153,6 de base octal a decimal:

(1*8^2)+ (5*8^1)+ (3*8^0)+ (6*8^-1)=64+40+3+6/8=107,75

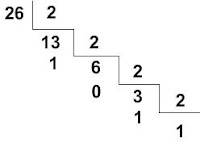
Conversión de un decimal a un binario

Se divide el
decimal entre dos consecutivamente y los residuos obtenidos de cada división se
escriben inversamente.

Ejemplo:

Donde el resultado seria 11010